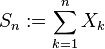2012-05-27

A/Bテストの数理 - 第3回 [補足]：仮説検定の概念を改めて考える -

統計数学 A/Bテスト

※ 第3回のブログを読んだけども，結局テスト（仮説検定）ってよくわかんないと言われるので，テストの概念をもう少し丁寧に説明することにした。特に「標本平均と母平均」，「帰無仮説を棄却すること」，「帰無仮説が棄却できないと何も言えないこと」について，焦点を当てている。

スケジュール

第1回 [読み物]：『人間の感覚のみでテスト結果を判定する事の難しさについて』：人間の感覚のみでは正しくテストの判定を行うのは困難である事を説明し，テストになぜ統計的手法が必要かを感じてもらう。
第2回 [読み物]：『「何をテストすべきか」意義のある仮説を立てるためのヒント』：何をテストするか，つまり改善可能性のある効果的な仮説を見いだす事は，テストの実施方法うんぬんより本質的な問題である（かつ非常に難しい）。意義のある仮説を立てるためのヒントをいくつか考える。
第3回 [数学]：『テストの基本的概念と結果の解釈方法について』：テストの基本的な数学的概念を説明し，またテスト結果をどのように解釈するのかを説明する。
第3回補足 [数学]：『仮説検定の概念を改めて考える』：テストの概念をもう少し丁寧に説明する。
第4回 [数学]：『実分野における9個のテストパターンについて』その1，その2：オンラインゲーム解析とキャンペーン事例に見る，テストにおける統計量の計算について説明する。
第5回 [数学]：『実際にテストを体感する』：いくつかのテスト事例に対し，サンプルデータを提供し実際に統計量の算出を行ってもらう。新シリーズ：「Treasure Data Analytics」の枠組み内で紹介することになりました。

母集団と標本について

統計学ではほとんどの場合，今手元にあるデータは全て「標本」であると考える。標本とは，「母集団」と呼ばれる全体から抽出された一部分である。例えば完全失業率は，日本国民全体（母集団）の中からランダムに抽出された10万人（標本）に基づいて算出される。A/B テストで得られたAとBのそれぞれのコンバージョン数などのデータもまた標本でしかない。

母平均と標本平均について

「平均」という言葉には実は2種類の意味がある。「母平均」と「標本平均」である。この違いの認識は非常に重要であるが，少なからずの人は「標本平均」を「母平均」と混同しているように思われる。

「母平均」というのはまさに母集団全体から求められた平均であるので，言わば真の平均値であり，かつこれは"定数"である。

一方「標本平均」というのは，母集団から"たまたま"集められた標本による平均であるので，必ずしも母平均とは一致しない。かつ，再度標本を取り直せばその値さえも変わってしまう。つまり標本平均とは "確率変数"である。

例：今，毎回 0 から 9 までの数字が独立かつランダムに選ばれるプログラムから，5個の数字を取ってくるという行為を2回行うとする。この時，

1回目は { 1, 4, 8, 3, 1 }，
2回目は { 5, 8, 2, 7, 0 }

であったとする。この場合（母集団 { 0,1,2,3,4,5,6,7,8,9 } に対して），

母平均： (0+1+2+3+4+5+6+7+8+9) / 10 = 4.5
1回目の標本平均： (1+4+8+3+1) / 5 = 3.4
2回目の標本平均： (5+8+2+7+0) / 5 = 4.2

となり，これら3つの平均はいずれも異なっている。

大数の弱法則，中心極限定理

ただ僕たちは経験的に，標本数が大きければその標本平均は母平均にかなり近くなること（大数の弱法則）を知っている。また「多数の標本を抽出して標本平均を求める」試行を 1 セットとすると，これを数セット行ったときには，多くの標本平均が母平均の近くに密集するであろうこと（中心極限定理）も何となく知っている。

標本抽出における重要なルール：「同一」・「独立ランダム」

ところで，母集団から標本を得る際には，忘れてはいけない重要な仮定がある。それは「同一」かつ「独立ランダム」に標本を抽出してくることである。

「同一」というのは同じ母集団から抽出してくるということである。

「ランダム」に抽出するというのは，母集団から偏り無くまんべんなく抽出してくることである。そうでない場合というのは，例えば労働調査では，特定の県に偏って標本を取得することに該当する。この場合，母集団を良く代表する標本平均が得られたとは言いにくい。
「独立に」抽出するというのは，標本同士が無関係であるということである。層で無い場合というのは，例えば労働調査では，まず最初に選んだ人に次の人を紹介してもらう，といった形で標本を取得していくことに該当する。独立で無い標本というのは傾向がどうしても似通ってしまうので，これも全体を良く代表する標本平均は得られにくい。

「AとBの母平均に差があるか」という問題に対するアプローチ

A/Bテストにおいて「AとB に違いがあるか」という問題は，「AとBの母平均に差があるか」という問題である。これに対するアプローチは，まず十分な数の標本からの標本平均を計算し，これを母平均の替わりをさせようとするところから始まる。

しかし，標本平均は"確率変数"であったので同じテストを複数回行うならば，標本平均 $\bar{X}_A$ と $\bar{X}_B$ はだいたい各母平均の近くにばらつくものの，その位置関係・距離関係は毎回異なるのである。

ここで重要なのは，AとBの母平均を知り得る事はできない事である。あくまでもA, B の標本平均と標本分散しかわからない。このような状況で「母平均の違い」を判定することは本質的に難しい問題であると言える。下図は母平均が同じ/違う場合での $\bar{X}_A$ と $\bar{X}_B$ の位置関係のいくつかのケースを書いている。※ 以降では A と B の標本数は十分に大きいと仮定する。（クリックで図を拡大できる）

f:id:doryokujin:20120527091658p:plain

左図は母平均が同じ（ここではあくまで母平均の違いについて関心があるので，分散は異なっていても良い）場合。A, Bの標本数が十分に大きければ，得られる各標本平均は同じ値の母平均の近くでばらつくので標本平均間の距離も小さくなる傾向がある。
中図は母平均が異なる場合。得られるA, Bの標本平均は，各母平均の近くでばらつくので，標本平均の距離は自然と離れている傾向がある。
しかし右図のように母平均が異なる場合でも，"たまたま" A, Bの標本平均の距離が小さくなるようなケースが得られる場合もある。また逆に，母平均が同じ場合でも，"たまたま"標本平均の距離が離れる場合もある。この場合は厄介である。

では，どのようにしてAとBの真の「違い」を判断すれば良いのであろうか？A, B の標本平均がどれくらいの距離内におさまっていれば良いのだろうか？

帰無仮説を持って棄却する，というアプローチ

ここから前に進む方法は，まずは「母平均が等しい」と置いてみることから始まる。そのように仮定することで，2つの標本平均から新しい統計量 T を作ることができるのだ。この T もまた実験の度に変動する確率変数であるが，T は母平均が等しいという仮説の下で，平均 0，分散1の標準正規分布に従う。しかしこの仮定が不適切な場合は T はこの分布のはるか両端に追いやられることになる。つまり統計量 T への変換は「標本平均の差」が元々大きければ大きいほど両端遠くへ，小さければ小さいほど母平均値 0 の近くにばらつくようにする変換なのである。

また，T の従う分布は言わば「母平均が 0 であるという帰無仮説の支持率」を示す診断と考えて良い。「有意水準」というのは「この値以下の支持率なら帰無仮説を疑う」任意の値である。有意水準 0.05 というのは，「T の支持率が5%以下ならば帰無仮説を受け入れない」ことを意味する。

A,B の母平均が同じ場合

f:id:doryokujin:20120527155847p:plain

Case1 は母平均が同じで，共に母平均周りに標本平均がとれた場合。この場合，変換後の T は 0 の近くに移動する。この時の帰無仮説の支持率は非常に大きくなる。
Case2, Case3 では"たまたま"いずれかの標本平均がその母平均から離れた値であった場合だ。この場合は標本平均の差は大きくなり，変換後では両端にとばされてしまい，支持率は低いと見なされてしまう。（第一種の誤り）

A,B の母平均が異なる場合（μ_A < μ_B）

f:id:doryokujin:20120527160124p:plain

A, B の母平均が異なり，かつ μ_A < μ_B の場合である。

Case4 の場合はもとの母平均の違いを標本平均が良く表しているために，変換後の T は右端へ追いやられる。これによって帰無仮説の支持率は低くなり「μ_A = μ_B」という帰無仮説は棄却され，「AとBには有意な差がある」と判断できる。
Case5, Case6 は厄介である。本来母平均が異なっていながら標本平均の差は近くなってしまっている場合だ。この場合は帰無仮説を支持し，棄却できないという「第二種の過り」を犯してしまうことになる。

A,B の母平均が異なる場合（μ_A > μ_B）

A, B の母平均が異なり，かつ μ_A > μ_B の場合である。

f:id:doryokujin:20120527160448p:plain

Case8, Case9 は先ほどと同じく，「第二種の過り」を犯してしまう例である。

A,B の母平均が異なる場合（μ_A < μ_B）：片側検定

f:id:doryokujin:20120527160543p:plain

実は片側検定という考え方がある。AとBが単純に「違いがある」という対立仮説を作るのでは無く，「母平均Bの方がAよりも大きい」という対立仮説を立てる方法である。この場合「μ_A > μ_B」である事は全く関心が無いので，変換後の T が右側に飛ばされることがのみが棄却の動機になる。この場合の有意水準 0.05 というのは棄却域を，今まで両端併せて 5% の領域と考えていたものが，今度は右側だけ考えて全体の 5% の領域となる。同じ値 T でも両側検定と片側検定の場合ではp-値が異なってくる。

「帰無仮説を棄却できない→何も言えない」というロジックについて

さて，帰無仮説を棄却できない場合は「AとBは同じ」と結論づけるのではなく，「何も言えない」という結論をするべきだと何度も行ってきたが，ここで改めてその理由を考えてみよう。

上図の Case5, Case6, Case8, Case9 をもう一度見て欲しい。このケースは本来AとBに差があるのに棄却できなかった第二種の誤りの例であるが，これらがどれくらいの確率で起こりうるのかは全く未知なのである。もし本来異なるのに同じと判断してしまう確率が 30% だったらどうしよう？「同じである」と判断しても，30% で間違っているのだからテストの信憑性は全く無くなってしまう。このように，帰無仮説を容認することは，未知の確率で起こる第二種の誤りを内在することになってしまうので，精神衛生上大変よろしくないである。「何も言えない」という判断は，これよりはむしろ無難な判断をしているといえる。

2012-05-25

A/Bテストの数理 - 第4回：実分野における9個のテストパターンについてその2 -

数学統計 A/Bテスト

（前ページからの続き）

2. Hypothesis-Driven Testing 〜キャンペーン施策を事例に〜

事例6. （A/Bテスト：2つの比率の差のテスト，ただし排反データ）

問『あるメーカーAは新しいビールXを開発した。今，斬新なデザイン1を採用するか無難なデザイン2を採用するかを決めかねている。そこで実際にあるお店で300人の買い物客にどちらのデザインが良いかを選んでももらう実験をした。結果はデザイン1が163人，デザイン2が137人であった。さて一見デザイン1の方が人気のようであるが，優位な差が見られるだろうか』　

解：デザイン1の比率を $p_1$ ，デザイン2の比率を $p_2$ とする。n = 300, $\tilde{p}_1$ = 163 / 300 = 0.542， $\tilde{p}_2$ = 137 / 300 = 0.457 である。

帰無仮説：「p_1 = p_2 (= p)」，対立仮説：「p_1 ≠ p_2」

統計量：帰無仮説の下で，

$T=\frac{(p_1-p_2)}{(1/n)\{(p_1+p_2)-(p_1-p_2)\}^2}$ は標準正規分布に従う。 $p_1$ ， $p_2$ を標本比率 $\tilde{p}_1$ ， $\tilde{p}_2$ で置き換え，

$T=\frac{(0.542-0.457)}{(1/300)\{(0.542+0.457)-(0.542-0.457)\}^2}=1.540$

よって p-値は，pnorm(1.540) = 0.06 > 0.025 。

∴ 帰無仮説は棄却されず，デザインに差があるとは言えない。

事例7. （2つの母平均の差のテスト）

問：『今度はライバルメーカーBのビールYを用意し，220人の客に両者を飲んでもらいそれぞれのビールに 10 段階評価を付けてもらったところ，以下のテーブルを得た。ビールXの方が評価が良さそうであるが，ビールXとYの間には評価に差があると言えるか』

n	ビールＸの評価（x_i）	ビールＹの評価（y_i）	d(=x_i-y_i)	d^2
1	8	6	+2	4
2	6	7	-1	1
3	9	5	+4	16
...	...	...	...	...
220	8	6	+2	4
計	-	-	+308	1012

解：ビールXの平均評価を $\mu_x$ ，ビールYの平均評価を $\mu_y$ とし，その差の平均を $\mu_d$ とする。標本数 n = 220, $\bar{d}=\frac{\Sigma d}{n}=\frac{\Sigma(x_i-y_i)}{n}$ 標準偏差 $s_d=\sqrt{\frac{\Sigma d^2-n\bar{d}^2}{n-2}$ とする。

帰無仮説：「 μ_d = 0」，対立仮説：「 μ_d ≠ 0」

統計量：帰無仮説の下で，

$T=\frac{\bar{d}}{s_d/\sqrt{n}}$ は標準正規分布に従う。

$T=\frac{1.4}{1.63/\sqrt{220}}=12.74$ 。

よって p-値は，pnorm(12.74) = 0 < 0.025 。

∴ 帰無仮説は棄却され，ビールの評価には有意な差があると言える。

事例8. （ブランディングスイッチ：対称性の適合度検定）

問：『メーカーA は大規模なイベントを実施し，ブランディング効果の向上を図ろうとした。以下は175人に対して実施した，イベント実施前と後の，ライバル含む 3 メーカーでの好みブランドのアンケート結果である。さてさて，このキャンペーンによって有意な好みの推移が起きたであろうか。』

f:id:doryokujin:20120525130854p:plain

解：

帰無仮説：「 $p_{ij}=p_{ji},\qquad\qquad 1\leq i\leq j\leq 3$ 」

統計量：帰無仮説の下で，

$\tilde{p}_{ii}=y_{ii}/n$ ， $\tilde{p}_{ij}=\tilde{p}_{ji}=(y_{ij}+y_{ji})/(2n)$ は最尤推定量。

$T=\Sigma_i \Sigma_j \frac{\left(y_{ij}-\frac{y_{ij}+y_{ji}}{2}\right)^2}{\left(\frac{y_{ij}+y_{ji}}{2}\right)}$ は $\chi^2(\n)$ に従う。a をカテゴリ数として， $\n={a \choose 2}$ である。

$T=\frac{(1-12)^2}{(1+12)}+\frac{(1-12)^2}{(1+12)}+\frac{(5-3)^2}{(5+3)}=19.2$ ， $\n=3$ 。

よって p-値は，chisq_(19.2, 3) = 0.03 < 0.05 。

∴ 帰無仮説は棄却され，ブランドの推移があったといえる。

3. その他

事例9. （小標本の母比率の検定）

問：『シーズンも後半にさしかかった頃，最近まで打率 .350 の首位打者であったイチローは，ここにきて20打数3安打と振るわなくなり，首位打者の座が危惧されている。さて最近のイチローの成績はとりわけ悪いといえるだろうか，それともたまたまであろうか』

解：最近の打率を p とする。最近の打席数を n，実現値を t とおく。ここでは n =20, t = 3 となる。標本数が少ないことに注意する。

帰無仮説：「p = p_0 (= 0.35)」，対立仮説：「p < 0.35」

統計量：帰無仮説の下で，

$T=\frac{m_2p_0}{m_1(1-p_0)}$ は $F(m_1,\qquad m_2)$ に従う。今， $m_1=2(t+1)=2(3+1)=8,\qquad m_2=2(n-t)=2(20-3)=34$ なので，

$T=\frac{34*0.4}{8*(1-0.4)}=2.833$ は F(8, 34) に従う。

よって p-値は，pf(2.833, 8, 34) = 0.016 < 0.025 。

∴ 帰無仮説は棄却され，イチローは最近とりわけ成績が悪いと言える。

※ 仮に帰無仮説が棄却できなかった時は成績に関して「何もわからない」ことになる。

事例10. （無相関検定，相関と因果）

（「明解演習数理統計」より，面白い問題があったので利用させてもらった。）

問：『「馬鹿はカゼをひかない」という俗説の信憑性を統計学的に立証しようとよくカゼをひくM君が彼の学友25名を任意抽出して，最近1年間にカゼにかかった回数と数学の成績との相関関係を計算したら，なんと0.41であった。カゼの回数と数学の成績は関係があるといえるか。』

解：母相関係数を ρ とする。

帰無仮説：「ρ = 0」，対立仮説：「ρ ≠ 0」

統計量：帰無仮説の下で，

$T=\frac{\sqrt{n-2}r}{\sqrt{1-r^2}}$ は $t(n-2)$ に従う。今，n = 25, r = 0.41 なので

$T=\frac{\sqrt{25-2}*0.41}{\sqrt{1-0.41^2}}=2.156$

よって p-値は， t(2.156, 23)=0.0209 < 0.025 。

∴ 帰無仮説は棄却され，カゼの回数と数学の成績は相関があると言える。

※ しかし，ここで注意すべきはたとえ結果から相関関係は導かれても，因果関係を導いたことにはなっていないということである。相関は言えても因果：「数学の成績が悪い【から】カゼの回数が少ない」i.e.「馬鹿はカゼをひかない」とは言い切れないのである。

そもそもこの問題は因果関係：「馬鹿はカゼをひかない」をいう仮説を，無相関検定のみで立証しようとしたこと（相関関係は因果関係を含意しない）ところに誤りがある。因果関係の妥当性を示すには有意な相関（密接性）と時間性、普遍性、特異性、合理性を示す必要がある。

2012-05-25

A/Bテストの数理 - 第4回：実分野における9個のテストパターンについてその1 -

統計数学 A/Bテスト

スケジュール

第1回 [読み物]：『人間の感覚のみでテスト結果を判定する事の難しさについて』：人間の感覚のみでは正しくテストの判定を行うのは困難である事を説明し，テストになぜ統計的手法が必要かを感じてもらう。
第2回 [読み物]：『「何をテストすべきか」意義のある仮説を立てるためのヒント』：何をテストするか，つまり改善可能性のある効果的な仮説を見いだす事は，テストの実施方法うんぬんより本質的な問題である（かつ非常に難しい）。意義のある仮説を立てるためのヒントをいくつか考える。
第3回 [数学]：『テストの基本的概念と結果の解釈方法について』：テストの基本的な数学的概念を説明し，またテスト結果をどのように解釈するのかを説明する。
第3回補足 [数学]：『仮説検定の概念を改めて考える』：テストの概念をもう少し丁寧に説明する。
第4回 [数学]：『実分野における9個のテストパターンについて』その1，その2：オンラインゲーム解析とキャンペーン事例に見る，テストにおける統計量の計算について説明する。
第5回 [数学]：『実際にテストを体感する』：いくつかのテスト事例に対し，サンプルデータを提供し実際に統計量の算出を行ってもらう。新シリーズ：「Treasure Data Analytics」の枠組み内で紹介することになりました。

（※ [読み物] は数学知識を前提としない内容で [数学] は数学知識をある程度前提としたおはなし。）

はじめに

様々なテストパターンを，オンラインゲーム解析とキャンペーンの事例で説明する。また前者におけるテストを "Data-Driven"な，後者を"Hypothesis-Driven"なテストと位置づけて，特に前者のテストは日々のデータ解析において「傾向検知」「異常検知」自動アラートの役割を果たしてくれる可能性がある事を説明する。

（ところで，日常のデータ解析にテストを常時活用することを僕は「TDD: Test Driven Data Mining」と呼んでいる。）

全ての問題で共通においている前提

※ 検定方向ついて

以下で紹介するテストは全て両側検定としている。両側検定についてはこちらを参照されたい。両側検定にする理由は，(1) 片側より棄却されにくいこと，(2) 信頼区間を同時に求める際に，棄却域と信頼区間が交わるような矛盾を極力避けるため。（ただし信頼区間についてはここでは取り上げない。）

※ 有意水準について

有意水準は全て 0.05 としている。

※ サンプルサイズについて

計算する統計量とそれの従う分布（特に標準正規分布か t 分布かで）はサンプルサイズによって異なってくる。ここでは「大標本」を n > 100 または n_1 + n_2 > 100 ，それ以外を「小標本」とみなす。ただし，母比率の検定は n > 30 を大標本とする。

結果の解釈方法について

第3回の最後にも紹介したが，テストの思考フレームワークは以下に統一される：

棄却を目的として，帰無仮説をこしらえる。
帰無仮説の下，標本からある分布（正規分布・t分布・F分布・χ^2分布など）に従う統計量 T を求める。
統計量 T がその分布の元で稀なケースかどうかをチェックする。
稀なケースであり，帰無仮説を疑う方が妥当であると判断できる場合は帰無仮説を棄却し、対立仮説を採択する。そうでないなら何もわからないと判断する。

この「稀なケース」と判断する手段について，p-値の役割と共に説明したい。

p-値とは「帰無仮説の下で実際にデータから計算された統計量よりも極端な（大きな）統計量が観測される確率」で表される。これは例えば p-値が 0.05 の時，「あなたが計算した計算量 T が（仮定する）分布から得られる確率は 0.05 である」と述べていることになる。テストのスタンスは帰無仮説を棄却する事であった。つまり p-値が小さければ小さいほど，T がこの分布に従っているという帰無仮説をより強く疑うことができる。

ここでは「稀なケース」と判断する場合には，両側検定では p-値が 0.025 より小さいときとする。（有意水準 0.05 の両側検定。）

f:id:doryokujin:20120525103858p:plain

統計量Tにおける p-値は x>T なる区間の面積。この区間から値が得られるのは「非常に稀」考えられる。標準正規分布においては T=1.96 の時，p-値は 0.025 となるので，T が1.96 より大きければ（あるいは反対側，T が -1.96 より小さければ）この分布において「稀なケース」と判断する。

Hypothesis-Driven Testing と Data-Driven Testing について

テストにはその実施方法において大きく2つに分類できる。「Hypothesis-Driven Testing」と「Data-Driven Testing」である。

Hypothesis-Driven Testing

A/Bテストや実験計画法に代表されるこの方法は，

(1) 仮説を立て，(2) 実験計画を立て，(3) 実験を実施，(4) 結果からテストを行う

というアプローチを取る。このアプローチのメリットは，始めに検証したい仮説がはっきりしているために厳密なテストを行いやすいことである。ブロック化や完全無作為化，あるいは複数の因子があるならばその交互作用も考慮に入れた上での計画が設定でき，系統的な誤差などの影響を受けにくくできる。一方デメリットは，まず何より仮説ありきであること，毎回の実験コストがそれなりにかかることなどによってそれほど気軽に行えないというところである。

Data Driven Testing

一方データ解析からスタートするテストがある。それは，

(1) 解析によって通常とは異なる傾向（異常）を発見する

(2) データに対してテストを行い，有意な違いがあるのかを統計的に確かめる

(3) 有意な違いが見られる場合は，解析によってその原因や要因を追求する

(4) 結論を出す，または解析不十分で仮説レベルにとどまるなら Hypothesis-Driven Testing を実施する

というアプローチである。例えばオンラインゲームの文脈で言えば，今日の課金分布やセグメント間の分布の傾向，過去のそれと異なるか否かをテストによって見つけ，その原因を分析し，結論を導いていく。

この場合のメリットは既に実験結果と見なせるデータが揃っているために，データを得るための実験ステップが無いことが挙げられる。デメリットは正確なテスト（標本のランダム性や独立性が不十分など）が行えない事である。

1. Data-Driven Testing 〜オンラインゲーム解析を事例に〜

ユーザー数百万人を誇るあるオンラインゲームがある。このサイトの全ユーザーの中から 1/1000 程度のユーザーの属性情報を独立かつランダムに取得できるとする。また，データベース上の課金テーブルにも自由にアクセスでき，これらサンプルユーザーの課金情報がいつでも参照できる状況にあるとする。

事例1. （母分散未知の母平均テスト）

問：『サンプルユーザー1000人の平均年齢を計算してみると，36.4歳，標本不偏分散は 15.0 であった。日本のゲーム全体でのユーザーの平均年齢が 34歳であるとするなら，このゲームの全ユーザーの平均年齢は，全ゲーム平均に比べて異なると言えるか。』

解：サンプルユーザーにおける平均を $\bar{X}$ ，標準偏差を $s_d$ とする。また，全ゲームでの平均を μ とする。

帰無仮説：「 $\bar{X}-\mu=0$ 」，対立仮説：「 $\bar{X}-\mu\neq0$ 」

統計量：帰無仮説の下で，

$T=\frac{\bar{X}-\mu}{s_d/\sqrt{n}}$ は標準正規分布に従う。

$T=\frac{36.4-34}{15/\sqrt{1000}}=5.06$ 。

よって p-値は，pnorm(5.06)=2.10e-07 < 0.025。

∴ 帰無仮説は棄却され，全ゲーム平均とは異なると言える。

事例2. （適合度検定）

問：『今度はサンプルユーザーの年齢を，10歳ごとの年代に分けて集計してみると以下のテーブルが得られた（有効数 832人）。こうして眺めて見ると，10代, 20代, 30代, 40代, 50代の人数比が 3 : 3 : 9 : 1 （メンデルの法則）のようになっているように見える。年代によるこの人数比の仮説が妥当かどうか確かめよ。』

カテゴリ	10代	20代	30代	40代	合計
観測個数	146	163	479	44	832

解：以下の様なテーブルを作る。

カテゴリ	観測個数 n_i	理論個数 m_i	n_i-m_i	(n_i-m_i)^2	(n_i-m_i)^2/m_i
10代	146	156	-10	100	0.6410
20代	163	156	7	49	0.3141
30代	479	468	11	121	0.2585
40代	44	52	-8	64	1.2308
計	832	832	0	-	2.4444

帰無仮説の下でカテゴリ数を a とする。

帰無仮説：「ユーザー数の年代分布の比率は 3 : 3 : 9 : 1 である」

統計量： $T=\Sigma_{i}\frac{(n_i-m_i)^2}{m_i}$ は自由度 a-1 のχ^2 分布に従う。テーブルより T=2.444 。

よって p-値は，pchisq(2.444,3)=0.485 > 0.05。

∴ 帰無仮説は棄却されず，年代ごとの人数比率は 3 : 3: 9 : 1 に従っているとは言えない。

事例3. （独立性の検定）

問：『年代による分類に加えて，今度はゲームプレイ時間を「1時間以内」「1〜3時間」「3時間以上」と分類し，年代と併せてテーブルを作ってみた（有効数360）。さてさて，年代とプレイ時間に関係があると言えるだろうか』

観測値テーブル n_ij

カテゴリ	10代	20代	30以上	計
1時間以下	25	103	52	180
1～3時間	16	39	17	72
3時間以上	19	38	51	108
計	60	180	120	360

解：

帰無仮説：「年代とプレイ時間は無関係である」

統計量：帰無仮説の下で，以下の期待値（最尤推定値）テーブル m_ij を作る。

カテゴリ	10代	20代	30以上	計
1時間以下	30	90	60	180
1～3時間	12	36	24	72
3時間以上	18	54	36	108
計	60	180	120	360

帰無仮説の下で，カテゴリ数を a×b として

$T=\Sigma_{i,j}\frac{(n_{ij}-m_{ij})^2}{m_{ij}}$ は自由度 (a-1)(b-1) のχ^2 分布に従う。

$T=\frac{(25-30)^2}{30}+...+\frac{(51-36)^2}{36}=18.349$ 。

よって p-値は，pchisq(18.349, 4) = 0.001 < 0.05 。

∴ 帰無仮説は棄却され，年代とプレイ時間は関係があると言える。

事例4. （A/Bテスト：2つの比率の差のテスト）

問：『5月は積極的な招待キャンペーンを行っており，特にそれによる招待成功率の向上が期待されていた。結果は 5月が 530人/2000人 = 26.5%で 4月の 230人/1000人 = 23.0%で効果があったように思われる。さて実際，このキャンペーンは成功だったといえるだろうか。つまり4月に比べて5月の招待成功率は高くなったといえだろうか。』

解：（統計量の導出方法は第3回参照）

$n_1=2000,\qquad n_2=1000,\qquad\bar{p}_1=0.265,\qquad\bar{p}_2=0.230,\qquad\bar{p}=(530+230)/(2000+1000)=0.253$ として，

帰無仮説：「p_1 = p_2 (= p)」，対立仮説：「p_1 ≠ p_2」

統計量：帰無仮説の下で，

$T=\frac{(\bar{p}_1-\bar{p}_2)}{\sqrt{\bar{p}(1-\bar{p})\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$ は標準正規分布に従う。

$T=\frac{0.265-0.230}{\sqrt{0.253*(1-0.253)*(1/2000+1/1000)}}=2.078$

よって p-値は，pnorm(2.078) = 0.019 < 0.025 。

∴ 帰無仮説は棄却され，前月よりも招待成功率は高くなったと言える。

事例5. （等分散検定）

問：『アイテムA とアイテムB の分布を見ると，平均売上額は同じであるようだが，アイテムAの分布は平均を中心に山を形成しており，逆にアイテムB は平均を中心に凹んだ谷を形成しているようである。今，標本分布の可視化が行えような状況で，アイテムA とアイテムB の違いを導き出すとするならば，どのような仮説のもとでテストを行えば良いだろうか。』

解：平均が同じだからといって，分布の形まで同じとは限らない。ここでのテストはアイテムA のアイテムB の分散が同じであるかどうかのテストを行うのが好ましい。例えばこの問題において，

-	課金者数	平均課金額	標準偏差
アイテムA	300	1503	235
アイテムB	400	1492	193

であったとする。アイテムA の分散を σ_a，標本不偏分散を U_a，アイテムBの分散を σ_b，標本不偏分散を U_b とおく。

帰無仮説：「σ_a = σ_b 」，対立仮説：「σ_a ≠ σ_2」

統計量：帰無仮説の下で，

$T=\frac{U_a^2}{U_b^2}$ は $F(n_a,\qquad n_b)$ に従う。

$T=\frac{(300*235^2)/(300-1)}{(400*193^2)/(400-1)}=1.48383$ 。

よって p-値は， pf(1.48383, 299, 399) = 0.0008 < 0.025 。

∴ 帰無仮説は棄却され，両者の分散には差があると言える。

Data-Driven Testingの神髄

データ解析者は日々たくさんのデータを眺め，その中から傾向を見いだし解析につなげるといった事が求められる。しかしながら，多くの種類またはカテゴリを持つあらゆるデータに対してそれを実行するのは極めて困難で有り，また人間の勘によって発見された傾向は，真実における偶然である事も多い。

データ解析の枠組みの中にシステム化され組み込まれたテストは，そういった解析の入り口である「傾向検知」アラートという役割を担う事ができる。

過去のデータの統計値を保存しておけば，本日/本期間の売上・ログイン・イベント参加率などのあらゆるデータに対してテストを自動実行できる。これによって検知された傾向の違いの原因を探り，真実を導くことは，今度は解析者の腕の見せ所である。

また，それは単に平均という1次元の値だけでは無く，適合度検定や独立性検定に見られるようにセグメント間の分布の違いをもテストしてくれる。その結果を持って解析者はまた，数理モデル化という手法を持って事象を記述する。

このように実社会において，テストの持つポテンシャルは多くの人が思っているより大きく，そして革新的である。「Treasure Data Analytics」シリーズのどこかで，この「Test Driven Data Mining」の魅力を，Fluentd と Hive への実装を持って紹介する予定である。

（続く）

2012-05-24

A/Bテストの数理 - 第2回：「何をテストすべきか」意義のある仮説を立てるためのヒント -

統計読み物 A/Bテスト

※ もはやテストの文脈と少しかけ離れた内容になっております，息抜きの読み物としてお楽しみ下さい…

スケジュール

第1回 [読み物]：『人間の感覚のみでテスト結果を判定する事の難しさについて』：人間の感覚のみでは正しくテストの判定を行うのは困難である事を説明し，テストになぜ統計的手法が必要かを感じてもらう。
第2回 [読み物]：『「何をテストすべきか」意義のある仮説を立てるためのヒント』：何をテストするか，つまり改善可能性のある効果的な仮説を見いだす事は，テストの実施方法うんぬんより本質的な問題である（かつ非常に難しい）。意義のある仮説を立てるためのヒントをいくつか考える。
第3回 [数学]：『テストの基本的概念と結果の解釈方法について』：テストの基本的な数学的概念を説明し，またテスト結果をどのように解釈するのかを説明する。
第3回補足 [数学]：『仮説検定の概念を改めて考える』：テストの概念をもう少し丁寧に説明する。
第4回 [数学]：『実分野における9個のテストパターンについて』その1，その2：オンラインゲーム解析とキャンペーン事例に見る，テストにおける統計量の計算について説明する。
第5回 [数学]：『実際にテストを体感する』：いくつかのテスト事例に対し，サンプルデータを提供し実際に統計量の算出を行ってもらう。新シリーズ：「Treasure Data Analytics」の枠組み内で紹介することになりました。

（※ [読み物] は数学知識を前提としない内容で [数学] は数学知識をある程度前提としたおはなし。）

はじめに

テストはその手法よりも，何をテストするかが重要であるが，そのための意義のある仮説を導くのは容易ではない。かと言ってテストを実施するコストを考えれば，適当な仮説を数打てば良い問題でも無い。良い仮説を立てるためには長年の経験や業務知識が必要であると言えるだろう。ただ，ここではそういった固有知識を必要としない汎用的な仮説を導くためのヒントを紹介する。

「クリックする」という観点から「選択する」という観点へ

例えば A/B テストの仮説と言えば，「リンクの色を変えたら〜」「画像を差し替えたら〜」「ボタンの文言を変えたら〜」といったものがメジャーである。

これらは皆，ユーザーがあなたのサイトのあらゆる場所を「クリックしている」という認識が根底にあり，これより導かれる仮説は，クリックされる物体に対して「目立ちやすさ」や「わかりやすさ」を改善することの効果に期待するものである。

A/Bテストの生事例蔵出し14パターン一気紹介（ポイント解説付き）

上記のサイトとはこのような "クリック指向" な仮説に基づく A/B テストの事例がたくさん載っていて非常に参考になる。（ただ p-値などでなく，CTRの変化だけで効果を述べている点で説得力に欠けると思われるのは，第1回に述べた通り。）

あらゆるものを「選択している」という観点で眺める

本ブログでは上記の観点とは異なり，次の様な観点を導入している。ユーザーがあなたのサイトのあらゆる場所・場面で「選択している」と考えるのである。

（例えば，あるWebサイトにアクセスすることや，あるリンクを押すこと，本を選ぶ事などは，「選択可能な集合体からの選択」である。自分のアバターを選ぶこと，アイテムを購入すること，ゲーム内で友達に挨拶することは，「可能な行動対象群の中からの選択」である。）

「選択」の裏には人間の意識が有り，心理がある。人間がどのような心理で「選択」を行うのか，その事がわかれば僕たちは自分たちのサービスを改善していく（または有利に進める）ことができるかもしれない。心理学や行動経済学などは，この人間の選択の心理を追求している学問である。そういった学問から導かれている結果・仮説を持ち込めるこのアプローチはそれなりに意義がありそうだと思う。

以下に挙げる心理学の研究はそれ自身があなたのサービスの改善につながる仮説にマッピングが可能なものとは限らないが，改善のための何かしらのヒントになり，かつ関心のあるものは実施の上テストしてその効果を確認してみてはどうだろう。

マジカルナンバー7±2

George Armitage Miller は，人間の短期記憶可能な物体や事実の数は 7±2 個であることを1956年の論文:「マジカルナンバー7±2：われわれの情報処理処理能力の限界」で述べている。人間はこれ以上の数になると知覚判断に影響を与えてしまうらしい。それは位置情報，音，味，物体の色，明るさといったあらゆる事においてである。

また，この研究は情報をブロック化することによって，知覚判断が改善されることも示唆している。確かにクレジットカードの12桁を覚えるのは難しいが，4桁ずつに区切った番号それぞれを記憶しておくことは前者のそれよりは簡単であろう。

このヒントを受けて，例えば「サイトのメニューの数を項目の削減や，カテゴリ細分化によって，1つのブロックを7個前後にすることでサイトのユーザビリティが向上する。」と考えてみることができる。（ただし，ユーザーは必ずしもメニュー項目を記憶する必要は無いので，この心理学的見地から導かれる実際の仮説はもっと練る必要がある。）

また，オンラインゲームの脈略で考えてみる。オンライン上の仲間とパーティを組み，互いに協力しながらダンジョンクリアを目指すようなゲームがあったとする。ゲーム全体のダンジョンクリア数を増やすことが良いことであるなら，

「常にお互いを認識しあえ，親密度の高いパーティを形成するための最適なパーティ人数はいくらが最適か？」に関するテストを7前後の数字を検証してみるのも。

「最上部」にあることの優位性

「最上部にある，と言うことが確かに他の位置のものよりも選択されやすいという仮説」の研究結果は多くある。著書「The Art of Choosing 」では，選挙の候補者が投票用紙に最上位に記載されている時とそうでない時の得票数の違いを検証し，平均的なアドバンテージが 2 %であることを述べている。

2000年のアル・ゴアとジョージ・ブッシュの選挙における得票数の差はほんの少しであった。多くの州で投票用紙の掲載準備が軽視されていたこの選挙においては，投票用紙の最上部の多くはブッシュであったことが知られているが，もしブッシュの名前が最上位で無かったとしたら，アメリカの社会は今と少し変わっていたのかもしれない。

アンカリング効果

人はあらゆる選択において「初期値」の影響を多大に受けている。

転職面接で前職の給料を聞かれた際に，200万円と答えるのと1000万円で答えるのではおそらく提示される価格は変わってくる可能性は結構ありそうだ。

このように人はアンカー（規準値・初期値）となる数字によって，その後の選択に影響を与えることが知られている。たとえそれが事実でないにせよ，統計的に基づいた意味のあるものでなくても，少なからずそのアンカーに引っ張られた選択を行ってしまう。

例えばあるレストランに対して5段階評価をつけるとする。また，その際に他の人の評価，あるいは全体の平均値が1つ見えているとする。アンカーが星5つの場合と，星1つであった場合では，あなたのつける星の数は変わってしまうかもしれない。

逆に言えば，このアンカーを利用して売り上げの改善が見込める可能性があるかもしれないということだ。

例えばPCを販売するあなたのサイトでは，複数のパーツ（CPU・メモリ・HDD）にグレードがついており，もちろんユーザーには高いグレードの構成にしてもらって購入させたい。もし，初期設定のグレードが全てにおいて最下位のものであったのなら，その初期のグレードを中程度のものに変更してみてはいかがだろう。また個々のパーツでの最適な初期グレードはいくらだろうか。これらを明確にするためのテストが必要だ。

ECサイトを運営するあなたのサイトには検索結果が 10 件，リストとして表示されることになっている。もしこの中でできるだけ高い商品を買ってもらいたいと思うなら，良いアンカーとなりうる商品を一番上に持って来る戦略は有効そうだ。

なぜなら，確かに購入という選択のもとでは単純な「最上位」効果は成立しえないだろうが，一番上の商品を最初に見ることによるアンカリング効果は少なからずあるはずだからである。良いアンカーを見つけるためのテストが必要だ。

情報の鮮明さがもたらす説得力

メアリー・ウィルソンは，論文「Information competition and vividness effects in on-line judgmentsInformation competition and vividness effects in on-line judgments」において情報の鮮明さの影響力の有意性を証明した。

陪審員役となった2グループの参加者は，被害者の最終弁論を収録したビデオを見さされる。ただしビデオはグループ間で弁護の鮮明さが異なっている。

グループA：被害者を弁護する議論が10の鮮明な主張とともに収録されたもの

グループB：同じ10の主張があまりぱっとしない論調で弁護しているもの

この実験では前者の説得には後者の2倍が有り，請求した賠償金額も異なるものであった。この研究に基づくならば，サイトのあらゆる場所の説明文をより具体的に魅力的に表現することは，ユーザーへの印象を高める効果があるということなので，テストする価値があるのかもしれない。

人に選択してもらう事の有効性

選択肢というものは多くの場合，自分が握っていることに安心感を持つ。しかし，時として他人に「選択してもらう」事の方が良い効果をもたらす場合がある。

この状況に遭遇するもっとも身近なケースは自信の「アバターの選択」である。各パーツ20以上もある選択肢の中から自分を的確に表現してくれるパーツを何度も選ぶことに少なからず負担を感じる人はいるだろう。かといって自分の分身を安易に選択できない。

実際，チュートリアルにおいてこのアバター選択における離脱率は他のステップよりも遙かに高い（もちろん選択肢の多さなど他の要因もあるだろうが）ケースが多い。しかしながら彼女や友人といった他人に選んでもらった場合には，自分に良く似たアバターをすんなりと選んでくれ，かつ満足度の高い結果になることもありうる。

「他人に選択してもらう」というシステムを作るのは必ずしも容易ではないが，それは，そのアクションにおける離脱率を有意に下げることができる可能性を含んでいるのかもしれない。

2012-05-23

A/Bテストの数理 - 第3回：テストの基本的概念と結果の解釈方法について -

統計数学 A/Bテスト

スケジュール

第1回 [読み物]：『人間の感覚のみでテスト結果を判定する事の難しさについて』：人間の感覚のみでは正しくテストの判定を行うのは困難である事を説明し，テストになぜ統計的手法が必要かを感じてもらう。
第2回 [読み物]：『「何をテストすべきか」意義のある仮説を立てるためのヒント』：何をテストするか，つまり改善可能性のある効果的な仮説を見いだす事は，テストの実施方法うんぬんより本質的な問題である（かつ非常に難しい）。意義のある仮説を立てるためのヒントをいくつか考える。
第3回 [数学]：『テストの基本的概念と結果の解釈方法について』：テストの基本的な数学的概念を説明し，またテスト結果をどのように解釈するのかを説明する。
第3回補足 [数学]：『仮説検定の概念を改めて考える』：テストの概念をもう少し丁寧に説明する。
第4回 [数学]：『実分野における9個のテストパターンについて』その1，その2：オンラインゲーム解析とキャンペーン事例に見る，テストにおける統計量の計算について説明する。
第5回 [数学]：『実際にテストを体感する』：いくつかのテスト事例に対し，サンプルデータを提供し実際に統計量の算出を行ってもらう。新シリーズ：「Treasure Data Analytics」の枠組み内で紹介することになりました。

（※ [読み物] は数学知識を前提としない内容で [数学] は数学知識をある程度前提としたおはなし。）

はじめに

　第3回ではテストの概念および解釈の方法について説明する。はじめに統計学を強力にサポートする確率論の「大数の弱法則」「中心極限定理」を紹介する。次に背理法に基づくテストの概念を紹介する。

Ⅰ. 統計学の基本スタンスについて

　第1回のコラムの続きから始めよう。コラムでは「僕たちは神ではないので答え（真の分布）を知ることはできない。よってその答えに対するヒント（サンプル）から答えを推定することしかできない。」と書いた。（「サンプル」は以後「標本」と呼ぶ。）

僕たちが手元に得られるデータというのは，たいていの場合が全体（母集団）の中の一部（標本）である事が多い。例えば労働調査データでは国民全員のデータでは無く，その中の10万人を独立ランダムにピックアップしたものである。

また，母集団の中からどのようなルール（分布）に従って標本が得られるのかもわからないことが多い。例えば（必ずしも平等でない）コイン投げでは，その母集団は {表, 裏} であることは知っていても表がどれくらいの確率で現れるのかはわからない。

世の中の多くの事象というのはこのように母集団や分布といったそれの本質的な部分を知ることはできず，そこから抽出される一部の標本の持つ（統計量と呼ばれる）情報からそれらを類推しないといけない。

統計学（特に推測統計学と呼ばれるが，ここでは統計と呼ぶことにする）というのは，得られている標本の統計量（標本平均や標本分散）をもとに全体（母集団）や真の分布をテスト（検定）したり推定したりする学問領域である。

Ⅱ. 現実と神の世界を結びつける架け橋：確率論

　統計は，現在手元に得られている標本から理論上の真の分布や母集団の情報（誰も知り得ない言わば神の世界）を想像しようとするが，そのためには「現実」と「理論」を結びつけるための何かしらのサポートが不可欠である。この大きな隔たりを極限の世界において華麗に結びつけてくれるのが「大数の弱法則」と「中心極限定理」と呼ばれる，確率論より導かれる性質である。

大数の弱法則

　 $X_1,X_2,...,X_n$ が，平均 $\mu$ ，分散 $\sigma^{2}\lt \infty$ の独立同一な確率変数列であるとする。今， $\bar{X}_n=(X_1+X_2+...+X_n)/n$ と置いたとき，任意の ε > 0 に対して，

$\lim_{n\rightarrow\infty}Pr\left(|\bar{X}_n-\mu|\geq\epsilon\right)=0$

が成立する。

大数の弱法則を大まかに言えば，標本数 n を十分に大きくしていけばその標本平均は定数 μ（真の平均）に限りなく近づいていくということを表している。コイン投げの文脈では，試行回数が多ければ多いほど実験で表の出る確率は，真の確率，つまり真のコインの姿をより鮮明に浮かび上がらせる事ができることを示している。

中心極限定理

　期待値 μ, 分散 $\sigma^{2}$ の独立同分布の確率変数列 $X_1, X_2,...X_k$ に対し、

$S_n := \sum_{k = 1}^n X_k$

とすると、 $S_n$ の標準化統計量 $Y=(S_n-n\mu)/\sqrt{n}\sigma$ は平均 0, 分散 1 の正規分布 N(0, 1) に分布収束する：

$P \Big( \frac{ S_n - n \mu }{ \sqrt{n}\sigma } \leqq \alpha \Big) \to \frac{1}{\sqrt{2 \pi }} \int_{-\infty }^{\alpha } e^{- \frac{x^2}{2}} dx$ 。

中心極限定理を大まかに言えば，標本数 n が十分に大きい状況では標本平均 $\bar{X}_n=S_n/n$ の分布は近似的に平均 $\mu$ , 分散 $\frac{\sigma^{2}}{n}$ の正規分布 $N(\mu,\qquad\frac{\sigma^{2}}{n})$ に従う事を述べている。（また， $S_n$ の分布は近似的に平均 $n\mu$ , 分散 $n\sigma^{2}$ の正規分布 $N(n\mu,\qquad n\sigma^{2})$ に従うとも言える。）

（大数の弱法則・中心極限定理の証明や確率収束・分布収束などの説明は省略するが，WEB参考資料としてはこれとこれがわかりやすい。）

コイン投げから観察する「大数の弱法則」と「中心極限定理」

　ではコイン投げを例に，大数の弱法則と中心極限定理の持たらす意味を考えてみることにしよう。今，平等なコインのコイン投げにおいて表の出る確率を実験によって求めてみる事にする。

※ コイン投げでは，i 回目のコイン投げにおいて表が出たときに1, 裏が出たときに0を取るような確率変数 $X_i$ を仮定すると，独立な変数列 $X_1,X_2,...,X_n$ の和 $S_n=X_1+...+X_n$ は表の出る回数を表していることになり，これを標本数 n で割った平均 $\bar{X}_n=S_n/n$ は表が出る確率を表している事になる。この時 $X_i$ をベルヌーイ確率変数とよび，和 $S_n$ の分布は二項分布に従う。

大数の弱法則

　大数の弱法則が意味するところは，コインを投げる回数を増やしていけば行くほど，実験から求めた表の出る確率は真の確率 1/2 に近づくことを示している。コインを n = 1,2,…,1000回独立に投げた場合の表の出る確率をグラフにしてみると，

f:id:doryokujin:20120522145544p:plain

のようになり，確かに n が大きくにつれて確率 1/2 に近くなっていく。Rにおけるサンプルコードはこちら。

中心極限定理

　標本数（試行回数） n を一定の値に固定し，毎回コインの表が出ると1, 裏が出ると 0 を標本として取る事にする。ここでは標本平均では無く標本の和，つまり表の出る回数 s を求める動作を 1 セットとして，これを数セット繰り返しヒストグラムを描くことで表の出る回数 s の分布を見てみることにする。下図は左から標本数を n = 10, 20, 1000としたときの分布を表している。標本数が大きいほど，表の出る回数の分布はこの定理より導かれる平均 n*0.5，分散 n*0.5*0.5 の正規分布を良く近似していることがわかる。（ここでセット回数は関心の中心では無い。ヒストグラムの様子を良く表すために n に応じて回数を増やしている）

f:id:doryokujin:20120522150353p:plain

また，パラメータ σ = 100 の指数分布においては，標本数 n が大きくなるほど，標本平均の分布がよく正規分布を近似している事がよくわかる。

f:id:doryokujin:20120522150938p:plain

Rでのサンプルコードはこちら。

標準正規分布

　標準正規分布は平均 0, 分散 1の正規分布である。この確率密度関数のグラフは以下の図様に表される。縦軸は出やすさの度合い，横軸の値は標本値（標準正規分布における横軸の値をz-valueと呼ばれる。）を表している。縦軸が最大となる標本値はその平均 0 に一致し，そこを頂とする山を形成している。これは標準分布に従った標本を抽出していく場合には，平均値 0 周りを中心に多くの標本値が得られることを意味している。100個の標本値の様子をRで実験してみよう。

table関数によって頻度集計を行うと，ほとんどの標本値が区間 [-2, 2] 内に落ちていることがわかる。実際，95% の標本値が区間 [-1.96,1.96] に落ちることになる。逆に言えば標本値が ±1.96 より離れた標本が得られる確率は両側合わせてたった 5%でしかない。もしあなたがちょうど1回の標本を抽出してみたときに，±1.96 より離れた標本が得られたならば，そのあまりにも希少な出来事に目を疑うことだろう。

f:id:doryokujin:20120522153317p:plain

（上記の標準正規分布の描画コードはこちら。）

Ⅲ. テストの概念について

　さて，テストの概念について説明できる準備が整った。ここまででわかっている事実を改めて並べて見よう。（以降で扱う標本は，独立かつ同一な分布から得られていると仮定する。）

[大数の弱法則] 標本数が十分大きければ標本平均は真の平均に近づいていく。必要ならば真の平均の代替としてこの標本平均を用いて計算を行う事が可能である。
[中心極限定理] 標本数が十分大きければ元の標本が従う分布が何であっても，標本平均の分布は近似的に正規分布 N(μ, σ^2/n) に従う。さらに標準化と呼ばれる変換を施すことによって得られる統計量 T は標準正規分布 N(0,1) に従う。
[稀なケース] 標準正規分布においてz-valueが区間 [-1.96, 1.96] 内に収まらない確率は 5% でしかない。（ここで 2. における統計量 T と3. における z-value は同じである。）

もし実験から得た標本から求める統計量 T が計算可能ならば，Tは標準正規分布からの1つの標本であると考えることができる。

定義

「テスト（仮説検定：Hypothesis Testing または有意性検定：Significance Test）とは，母集団または真の分布について設定した仮説の妥当性の判断を，標本を元に計算する統計量を元に一定の確率水準で判定する事である。」

概念

　A/Bテストの同型問題であるコイン投げの例では「コインAとコインBの表の出る確率は異なるはずだ」とういう仮説の下でテストを行う。今コインAの表の出る確率を p_a, コインBのそれを p_b とすれば，この仮説は数学的表現として「p_a ≠ p_b である」と表すことができる。しかし実際に設定する仮説は，その対となる「p_a = p_bである」の方になるので注意が必要である。（「p_a = p_bである」という仮説を帰無仮説，これに対立する「p_a ≠ p_bである」という仮説は対立仮説と呼ばれる。）

これには以下の様な理由がある。（主に最初の方が重要）

テストは背理法に似た論法を持って仮説の検証を行う。（背理法とはある主張を真としたとき，その主張に矛盾がある事を示すことでこの主張を否定する方法である。）よって支持する仮説は対立仮説に据える。
帰無仮説によって，母集団および真の分布についての何らかの設定がなされる。これによって中心極限定理を利用することができるようになり，標本から求めた統計量 T が標準正規分布に近似的に従う事が言える。統計量 T を求めるに当たって，不等号や≠を用いている設定よりも等号のみで成立している設定の方が遙かに計算が容易になる。

テストは棄却を目的とした帰無仮説「p_a = p_bである」の元に検証が行われる。もしこの仮説が妥当では無い（完全否定とは意味合いが異なる）と判断できる場合は帰無仮説を棄却し，対立仮説「p_a ≠ p_bである」の方をより妥当として採択する。

テストでは「否定」という言葉は使わずに「棄却」という言葉を使用する。また帰無仮説の「帰無」とは「棄却することを前提に設定されているので，無に帰す」という意味合いが込められている。

帰無仮説を棄却するということの意味

　（今後は区間 [-1.96,1.96] を「採択域」，採択域の外側を「棄却域」と呼ぶことにする。この言葉の意味はすぐに理解できるだろう。）

ではどのようにして帰無仮説を棄却するのだろうか？ここで標本分布の話を思い出して欲しい。帰無仮説の元では統計量 T は標準正規分布に従うが，その値が棄却域に入っているならばこのテストにおいては非常に稀な値を手にしてしまったことになる。

もし僕たちが真の分布を知っている神の立場であれば，この場合でも「稀なケースだったね」という話で済むだろうが，何せ僕たちは（仮定はおいているものの）真の分布を知らない。そのような立場からこの状況を判断するならば，「稀なケース」と考えるよりも「そもそも帰無仮説が正しくなかったのでは無いか」と考える方が妥当の様に思われる。

その考えのもと，T が棄却域に落ちるケースでは帰無仮説を棄却し，例えば「有意な差があると言える」と判断する。「有意」という言葉には「起こる確率が小さい場合には，それはめったに起こらないのでもしそれが起こったとすれば，それは偶然ではなく何か明白な意味が有ると考える方が妥当である」という意味合いが込められている。

ただ状況によっては棄却するか否かの厳しさ，つまり「妥当性の天秤」が異なってくることに注意が必要である。帰無仮説の元で稀なケースを観測する確率を α (ここではずっと α = 0.05 = 5%と置いてきた) とし，これを有意水準と呼ぶ。この有意水準を調整することによってこの妥当性の天秤を調整するのである。一般的に有意水準 α は 0.05 か 0.01 に設定される。後者はより起こりにくい確率を定義しているので，前者よりも帰無仮説を棄却しにくくなりより厳しいテストとなる。有意水準 0.01 の元では採択域は [-2.58, 2.58] と広くなるからだ。

第一種の誤り・第二種の誤り

　ただ，本当に稀なケースに遭遇していた可能性もありうる。帰無仮説を誤って棄却してしまう（これを第一種の誤りと呼ぶ）可能性だ。

テストにおいて最終的に導かれる判断には第一種の誤りの可能性を常に含んでいるために，「有意な〜」や「〜であると言える」という控えめな表現を用いる。逆に採択域に収まるケースでは，帰無仮説を棄却することはできないので「このテストからは何もわからない」という判定をする。ここで，”帰無仮説を採択する”という判定を行い，「〜は同じであると言える」などと言ってはいけない。

∵ テストにおいては先ほど紹介した第一種の誤りの他に，第二種の誤りの可能性も内在している。第一種とは逆で，「偽である帰無仮説を採択してしまう誤り」である。第一種ではその誤りの確率は有意水準に等しく，故に制御可能な誤りである。一方，第二種の誤りの方は制御不可能な誤りであり，その確率は未知である。故に安易に帰無仮説を採択する行為は，確率未知の第二種の誤りを容認してしまうことになるので安易に帰無仮説を採択することはできない，故に「何も言えない」という判定にするのである。

問：『今年，新型かもしれないインフルエンザ $\n_1$ が流行の兆しを見せている。もし過去に類を見ないタイプであればすぐに新薬を開発して流行を食い止めなければ大変な事になる。そこで， $\n_1$ が本当に新型かどうかを確認するために，患者の症状および血液検査の結果を，過去の似通ったインフルエンザ $\n_2$ が流行した際に取っていた結果と比較し，結果に差があるかどうかをテストすることにした。帰無仮説を「インフルエンザ $\n_1$ と $\n_2$ は同じである」とした時，第一種の誤りおよび第二種の誤りが何であるかを指摘し，それがもたらす影響を考え，どちらが重大な過ちであるかを考えよ。』

答：

第一種の誤り： $\n_1$ は過去のインフルエンザ $\n_2$ と「同じ」ものであったのにも関わらず，誤って「有意に違う」，つまり「 $\n_1$ は新型である」と判断してしまい，新薬の開発に無意味な研究費を投じてしまった。
第二種の誤り： $\n_1$ は過去のインフルエンザ $\n_2$ と「異なる」ものであったのにも関わらず，誤って「同じである」と判断してしまい，過去の効果のない薬を提供する判断を下したために流行が拡大し，より多くの人命が危機にさらされてしまった。

Ⅳ. A/Bテストにおける統計量の計算方法について

　（※ 統計量の計算とそれの従う分布について，興味の無い方は種々の公式だけ覚えて置けば良いので読み飛ばしてもらっても構わない。）

A/Bテストの同型問題のコイン投げで考える。コインAを n_a 回投げて表の出た回数を y_a，コインBを投げて表の出た回数を y_b と置き，ここでは標本数 n_a, n_b が十分大きいとする。また，それぞれの標本平均を $\tilde{p}_a=y_a/n_a$ および $\tilde{p}_b=y_b/n_b$ と置く。帰無仮説を「p_a = p_b (= p)である」とおく。これは2つの分布の差「p_a - p_b が 0 である」とも書ける。ところで正規分布には以下の様な良好な性質を持っている。

「 2つの独立な正規分布 $N(\mu_1,\qquad\sigma_1^2)$ および $N(\mu_2,\qquad\sigma_2^2)$ の和の分布もまた正規分布 $N(\mu_1+\mu2,\qquad\sigma_1^2+\sigma_2^2)$ に従う。」

これを利用すると，帰無仮説の下でコインAの分布 p_a とコインBの分布 p_b の差の分布もまた，平均 0 正規分布に従う事が言える。 $\tilde{p}_a$ と $\tilde{p}_b$ の差の分布の分布は，中心極限定理より近似的に

$N\left(0,\qquad\left(\frac{1}{n_a}+\frac{1}{n_b}\right)p(1-p)\right)$

に従う。帰無仮説の元で共通の確率 p を標本推定値

$\tilde{p}=\frac{y_a+y_b}{n_a+n_b}$

で置き換えることにすると，標準化した統計量 T は

$T=\frac{\tilde{p}_a-\tilde{p}_b}{\sqrt{(1/n_a+1/n_b)\tilde{p}(1-\tilde{p})}$

となり，この時 T は近似的に標準正規分布に従う。

サンプル数とサンプル数の偏りの影響

　第1回では，「テストの判定が（人間の感覚的に）標本数の大きさや，標本数で偏りで信念が揺らぐ」傾向にあるという事に触れた。これは先ほど求めた統計量 T が標本数 n_a および n_b の値に依存していることより正しくそれが言える。今回のA/Bテストで導かれた統計量は n_a や n_b が大きくなれば分母が小さくなり，統計量 T としては値が大きくなる傾向にある。これは区間 [-1.96, 1.96] からどんどん遠ざかっていく事を意味し，「とっても稀なケース」としてより確信度高く帰無仮説を棄却できる。

p-値

ところで，この「確信度」というのは「p-値」と呼ばれており，帰無仮説の下で実際にデータから計算された統計量よりも極端な（大きな）統計量が観測される確率である。標準正規分布に従う統計量が T=1.96 の時，有意水準 0.05 の元では p-値は0.025である（両側を併せると有意水準に一致する）。p-値が小さければ小さいほどより稀なケースが起きていることになり，故に帰無仮説が間違っていると考えることの確信度が高まる。p-値は帰無仮説を棄却する事の確信度，というあいまいな感覚値を数値化した有用な指標であると言える。

Ⅴ. まとめおよびその他のテストに関して

　ここではA/Bテストの例しか取り上げなかったが，テストは様々な種類がある。それによって計算する統計量 T と T に従う分布は異なってくる。今までは標準正規分布に従う統計量を用いてきたが，その他にも t 分布・F 分布・χ^2 分布に従う統計量が存在する。それらはどれも出発点は中心極限定理と標準正規分布にある。ただサンプル数の大小，または分散が既知か未知かによって計算することのできないパラメータが存在するので，それを四則演算によって巧みに打ち消すようにして作った統計量が t 分布や F 分布に従うのだ。ただし，基本的にはどのテストにおいても，その概念は変わることは無い：

大数の弱法則および中心極限定理がテストを強力にサポートする。
棄却を目的として，帰無仮説をこしらえる。
帰無仮説の下，標本からある分布（正規分布・t分布・F分布・χ^2分布など）に従う統計量 T を求める。
統計量 T がその分布の元で稀なケースかどうかをチェックする。（p-値はどれ位稀なケースか、言い換えればどれ位の確信度を持って帰無仮説を棄却できるかを計るための、あらゆる統計量において有用な指標である。）
稀なケースであり，帰無仮説を疑う方が妥当であると判断できる場合は帰無仮説を棄却し、対立仮説を採択する。そうでないなら何もわからないと判断する。
あらゆるテストは誤りの可能性を排除できない。また，第一種の誤り確率は有意水準に等しく制御可能であるが，第二種の誤りは制御不可能である。

興味を持たれた方は色々なパターンを調べて見て欲しい。また，第4回では他の様々なテストが事例とともに登場する。

2012-05-21

A/Bテストの数理 - 第1回：人間の感覚のみでテスト結果を判定する事の難しさについて -

読み物統計 A/Bテスト

データ解析の重要性が認識されつつある（?）最近でさえも，A/Bテストを始めとしたテスト（ = 統計的仮説検定：以後これをテストと呼ぶ）の重要性が注目される事は少なく，またテストの多くが正しく実施・解釈されていないという現状は今も昔も変わっていないように思われる。そこで，本シリーズではテストを正しく理解・実施・解釈してもらう事を目的として，テストのいろはをわかりやすく説明していきたいと思う。

スケジュール

スケジュール
- 第1回 [読み物]：『人間の感覚のみでテスト結果を判定する事の難しさについて』：人間の感覚のみでは正しくテストの判定を行うのは困難である事を説明し，テストになぜ統計的手法が必要かを感じてもらう。
- 第2回 [読み物]：『「何をテストすべきか」意義のある仮説を立てるためのヒント』：何をテストするか，つまり改善可能性のある効果的な仮説を見いだす事は，テストの実施方法うんぬんより本質的な問題である（かつ非常に難しい）。意義のある仮説を立てるためのヒントをいくつか考える。
- 第3回 [数学]：『テストの基本的概念と結果の解釈方法について』：テストの基本的な数学的概念を説明し，またテスト結果をどのように解釈するのかを説明する。
- 第3回補足 [数学]：『仮説検定の概念を改めて考える』：テストの概念をもう少し丁寧に説明する。
- 第4回 [数学]：『実分野における9個のテストパターンについて』その1，その2：オンラインゲーム解析とキャンペーン事例に見る，テストにおける統計量の計算について説明する。
- 第5回 [数学]：『実際にテストを体感する』：いくつかのテスト事例に対し，サンプルデータを提供し実際に統計量の算出を行ってもらう。新シリーズ：「Treasure Data Analytics」の枠組み内で紹介することになりました。
（※ [読み物] は数学知識を前提としない内容で [数学] は数学知識をある程度前提としたおはなし。）

はじめに

多くの人はA/Bテストについて色々と間違った解釈を持ってしまっているように思われる。その代表が，

「A/Bテストは，実施結果の判断（AとBに違いがあるか否か）を（統計量に基づく仮説検定を全く行わないで）人間が判断するものである」

と思われていることである。また何らかの統計的手法によってそれを行う事は何となく知っていても，

「A/Bテストは，統計的手法それ自信が完全な意思決定を行ってくれる（白黒はっきりしてくれるもの）ものではなく，最終的には人間の判断に委ねられるものである」

という認識は実際に実施してみないと気づかないことかもしれない。（前者と後者は矛盾するように思われるかもしれないが，後者は第3回で説明するのでそのときに理解してもらえるはず）。第1回は前者の部分，テストにおいて人間の感覚による判定がいかに難しいかを説明する。

題材：A/Bテスト

今回のゴールは「人間の感覚だけで次に挙げるいくつかのA/Bテストの結果を正しく判断できますか？できないでしょう？」という主張を理解してもらうことにある。

よくあるA/Bテストの事例を題材にしてみた：

Q.「あるトップページの1つのリンクを青から赤に変える事によってリンク先へのアクセス数が増えるのでは無いかという仮説を持っている実験者は，その違いをテストしてみることにした。そこでオリジナルのトップページ（A）と1つのリンクを赤にしたトップページ（B）を作成し，だいたいアクセスが半々に独立かつランダムに割り振られるようにして，A, Bそれぞれのアクセス数に対してそのリンクが実際に押された比率（Conversion Rate）を比較することにした。双方1000アクセス来た時点で比率を計算すると，Aが40%であったのに対しBは60%であった。さてこの結果を受けてAとBには本当に差があると言え，赤リンクにしたことに効果があったと判定できるだろうか。」

※ 現実問題などの具体的な問題を考える上で1番始めにすべきことは，問題をより単純な数学問題へすり替える事である。比率の差を比較するA/Bテストの類いは，以下のような単純なコイン投げの数学問題と同型である。（AとBが同じ数学的構造を持つとき，AとBを同型と呼ぶことにする。例えばこちらで定義した「コンプガチャ問題」と「Coupon Collector's Problem」は同型である。）

Q'.「表の出る確率がわからないコインAとコインBがある。表の出る確率をそれぞれ p_a, p_b とする。コインAとコインBは違う確率を持ったものであるという仮説を持っている実験者は，その違いをテストしてみることにした。コインA，Bをそれぞれ 1000回ずつ投げてみて，表の出る比率を比べることでそれを確かめようとしている。今，コインAの比率が 40%であったのに対しコインBの比率は 60%であった。この実験からコインAとコインBには違いがある(i.e. p_a ≠ p_b)と言えるだろうか。」

（※ A/Bテストのより一般的な定義（スケルトン）は第3回で与える。）

このA/Bテスト判定問題に関して，多くの人は以下のように答えるだろう：

「[根拠1] Aに比べてBは1.5倍も多く表を出しており，[根拠2] しかも1000回という十分なサンプル数がある。よってAとBには結果に明らかな違いがあり，赤リンク効果が実証されている！」

実はこの答えは正しく，人間の感覚もまんざらでは無いと思われた事でだろう。（そもそも，Bの方が数値的に良かったのであるので「効果があった」という答えしかないであろうと思う人もいるかもしれない。統計の背後には確率というものが常に存在しており，その"偶然"という要素の作用によって本来は効果に違いなんてなかったのに，たまたま数値的な違いが現れてしまったという事も有り得るのである。詳しくはコラム参照。）

次に上記問題のバリエーションを考えてみて欲しい。（類似の問題が並べられている故に解答に戸惑ってしまうかもしれないが，それぞれ独立した問題として考えて欲しい。）

Q1. コインA，コインBをそれぞれ 10回投げてみて，40％, 60％であったとき
Q2. コインA，コインBをそれぞれ 40回投げてみて，40％, 60％であったとき
Q3. コインA，コインBをそれぞれ 100回投げてみて，40％, 60％であったとき
Q4. コインA，コインBをそれぞれ 1000回投げてみて，40％, 60％であったとき（Q'. と同じ）
Q5. コインA，コインBをそれぞれ 1,000回投げてみて，48％, 52％であったとき
Q6. コインA，コインBをそれぞれ 1,000回投げてみて，47％, 53％であったとき
Q7. コインAを 20回，コインBを 80回投げてみて，40％, 60％であったとき

さて，答えは以下となる（最後に手計算とRでの計算結果を載せている）：

Q1. → 「差があるとは言えない」
Q2. → 「差があるとは言えない」
Q3. → 「差があると言える」
Q4. → 「差があると言える」
Q5. → 「差があるとは言えない」
Q6. → 「差があると言える」
Q7. → 「差があるとは言えない」

このバリエーション問題の難しい（間違える）のは，人間の感覚的な判断を揺るがす以下の要素が含まれるからである：

サンプル数が少ない場合：Q2, Q3のようにサンプル数が少ない場合。サンプル数が多い方が違いを見極めやすい事を感覚的には知っているが，数がどれくらいあれば良いのかはわからない。（そもそもサンプル数を増やすと，違いがあると言いやすくなるという根拠がどこにあるのかもわからないかも。）
比率の差が接近している場合：Q5., Q6のように比率が47%と53%や48%と52%のように接近している場合，（「微妙」という答えは無いため）違うと言える差の境界がわからない。
サンプル数が偏る場合：Q7のようにサンプル数が偏っている場合，双方の結果を平等に眺めることが難しくなる。（注:「サンプル数」= 「コインを投げる回数」）

このようにテストにおいて「違いの差」を考える際には上記のような人間の感覚が類推できる範囲を超えた，「サンプル数や双方の数の偏りとの関連の考慮」などが必要となってしまう。故に人間の感覚でA/Bテストの結果を判断するのは難しいのである。

現実社会での事例

では実社会で僕たちが，本来は差が無いと考えられる結果に動揺させられている事例を2つ程挙げてみよう。（計算方法はエントリー最後に掲載）

1. 失業率

現在，労働力調査は，全国で無作為に抽出された約40,000世帯の世帯員のうち15歳以上の者約10万人を対象とし，その就業・不就業の状態を調査している。

全数調査では無い失業率は，もう1回調査を行ってみればその数値が前と異なっていることは大いに有り得る。にも関わらず本来悪化したとは言いいきれない失業率の0.1ポイントの増加（悪化）に対しても悲観的に報じられるメディアによって国民は不安に煽られてしまう。

問:「前月: 4.9%, 今月: 5.0%とした時，前月比較で0.1ポイントの失業率の増加は悪化したと言えるか? 」

答: 「悪化したとは言えない」

2. 年収500万円と2000万円の人の違い

「手柄を社内にアピールするか否か」 (page2)

年収500万円の300人と年収2000万人の200人に対する調査結果の解釈について。中には以下の様に年収間で差があるとは言い切れない結果もある。

問:「手柄を社内にアピールするか否かの調査結果は，年収間で差があると言えるか」

答: 「差があるとは言えない」

※ 年収別の調査結果は，2×l 分割表の適合度検定の問題等，様々なテストを考える上で非常に興味深い。

コラム：テストに潜む ”偶然” のいたずらについて

統計の背後には必ず確率という概念が存在する。それを理解するために今度は僕たちはすでに答えを知っているという神の立場から，A/Bテストを考えてみることにしよう。

Case1: 『実はコインAとコインBは実は同じコインで，かつ表と裏が平等に出る（ p_a = p_b = 1/2 ）公平なコインである事を知っており，今これらのコインでテストしようとする実験者を眺めているとする。この時コインA, Bをそれぞれ10回投げた時，Aは表が出て4回出てBは6回出た。もう一度繰り返してみると，今度はAが2回，Bが8回であった』

Case2: 『今度はコインAの方がコインBより表が4倍出やすい（ p_a = 4/5, p_b = 1/5 ）とする。今これらのコインでテストしようとする実験者を眺めているとする。この時コインA, Bをそれぞれ10回投げた時，Aは表が出て4回出てBは6回出た。もう一度繰り返してみると，今度はAが2回，Bが8回であった』

Case1 の方は，10回のコイン投げるという実験を1セットと呼ぶなら，表が5回出るセットが最も多そうだけれども表が4回出ることも6回出るセットも十分に起こりうるだろう。よって実験者は「違いがあるとは言えない」と判断すべきと思うだろう。"偶然" Aの方は表が4回出てBの方は6回出た結果に対して，それを元が違うと判断するのは早計である，と。2回と8回出たケースに関しては，このセットはほとんど起こり得ないが確率 0 では無い。ただしこの場合は実験者は「違いがある」とまたも間違ってしまうが，答えを知らない立場からのその判断は賢明であると思うだろう。たまたま出にくい実験結果を得てしまった，運が悪かったねと言ってあげたくなる。（本来同じであることを違うと判断してしまうこの誤りは「第1種の誤り」と呼ばれていたりする。）

Case2 の方は，今度は本来コインは異なるものであるのに，4回と6回という結果を受けて実験者が「差が無いとは言い切れない」と判断しても仕方が無いと思うだろう。たいていはコインAとBで開きがあるケースが多いのに，運悪く両者の違いの小さなセットを得てしまったのだと。（違うのに同じと判断してしまうこの誤りは「第2種の誤り」と呼ばれていたりする。）

この2つのケースから言えるのは，答えを知らない立場の側が「賢明」と思われる判断を行っても，それが間違いであることが有り得ると言うことである。

僕たちは神ではないので答え（真の分布）を知ることはできない。よってその答えに対するヒント（サンプル）から答えを推定することしかできない。テストというのは統計的手法を持ってしても，偶然の ”いたずら” によって間違えてしまうこともあるのである。テストに対する統計的アプローチは，間違いの可能性は避けられないができるかぎり最適な方法を持って臨むことである。人間の感覚の判断というアプローチはこの偶然のいたずらによる影響と，「違い」の程度とサンプル数との関連を類推しきれない事の影響を受けてしまう故に，最適な方法とはほど遠いと考えられる。

問題の答え