コンプガチャの数理 -ガイドラインに基づいたゲームデザインその1-

4. 『コンプガチャの数理 -ガイドラインに基づいたゲームデザインその2-』

5月25日にコンプリートガチャガイドラインが策定され，コンプガチャに関して新しい規定が策定されたようだ。その中で現在可能なゲームデザインは以下に限定された。

『有料ガチャアイテムを含む特定の２つ以上の異なるアイテム等を全部揃えることを条件として、ソーシャルゲーム等で使用することができる景品類たる別のアイテム等を利用者に提供する方式をいう。なお、以下に該当するものを除く。』

利用者がアイテム等の種類を選択することによりその組み合わせを完成できるもの
異種類のアイテム等の組み合わせではなく、利用者が、同種類のアイテム等を一定個数揃えれば新規のアイテム等の提供を受けるもの
１点，２点，５点というように，異なる点数が付与されているアイテム等を利用者に提供し，合計が一定の点数に達すると，点数に応じて利用者が新規アイテム等の提供を受けるもの

今回は上記のガイドライン規定に従う形でコンプガチャに関する数学的ゲームデザインを考えてみようと思う。ところで数学的ゲームデザインとは，

『ある数学モデルのレールに沿ったゲームをデザインすることである。それによって，その背景にある種々の数学的性質を活用して優位な戦略を立てることが可能になる。』

と定義し，全てのルールと確率値を公開し，確率操作を行わない，フェアなゲームの下で考えられるものであった。

はじめに

まず，ガイドラインに 3. の許可がきちんと明記されていることは重要である。これが無ければ，点数を集めて白いお皿がもらえる春のお楽しみも無くなってしまうからだ。ただし，この問題に関してはあまり面白みが無いので今回は省略する。今回は 1. および 2. に基づいた数学的ゲームデザインを考える。

結論としては，1. については完全コンプを目指さなくても期待回数を大きく増やすようなデザインが可能であることを示す。2. については次回に詳しく紹介する。

1. 部分コンプリートモデル

さて，1. についてはどう解釈すれば良いのかわからないけれども，今回は勝手に以下の様に解釈する。以下に定義するモデルを『部分コンプリートモデル』と呼ぶ。

「全 m 種類のアイテムの中の任意の n (n<m) 種類のみ集めればコンプリートと見なす」

また設定の簡略化のために，とりあえず n 種類のアイテムが集まれば良いものとする。（特定の n 種類に限定するとコンプの確率は低くなる。）また全種類集めるよりも，その一部のみ集めるルールの方がコンプまでの期待回数も少なくなるのは明らかである。

この問題に関しても，前回と同じく「The Coupon Collector's Problem」の枠組みで考えることができる。つまり

a. 全アイテムで出現確率が等しい場合
b. アイテムごとに出現確率が異なる場合

で考えることができる。

a. 全アイテムで出現確率が等しい場合

全 m 種類のアイテムの出現確率が等しく 1/m の場合を考える。今， $X_i$ を新たな i 種類目のガチャが出るまでに買わないといけない数であるとする。また，m 種類のガチャを全て得るための回数を $X(m)$ とする。コンプまでに必要な期待回数 $E[X(m)]$ を求める問題は前回取り上げた問題である。この時の結果は，

$E[X(m)]=\Sigma_{i=1}^{m} E[X_i]=\Sigma_{i=1}^{m}\frac{m}{m-i+1}= m\Sigma\frac{1}{i}=mH(m)$

である。ここで調和数 $H(m)=\Sigma\frac{1}{i}$ と置いている。よって n 種類のアイテムを集めるのに必要な期待回数 $E[X(n)]$ は，

$E[X(n)]=m(H(m)-H(m-n))$

で良い。それではこの結果を用いて全20種類のアイテム ( m = 20 ) から，1〜20種類 ( n = 1... 20) コンプするのに必要な期待回数を見てみよう。

f:id:doryokujin:20120529171840p:plain

左は m = 20，右は m = 100 の時の部分コンプ種類数 n を横軸に，縦軸に期待回数をとった推移図。このように n 種類集めるのに必要な期待回数は n の増加とともに指数的に増加するものの，初めから n/2 程度では期待回数の増加はほぼ線形オーダーでしかない。部分コンプリートモデルでは，全体の半分や1/4 の種類集めれば良いモデルなのでこれはあまり好ましい状況では無い。

例えば前回紹介した AKB48 のポスターコンプモデルでは，44枚全て集めるには192個のCDを買う必要があったが，10枚で良ければCD11個で良い。ゲームをデザインする側としては，あまり刺激の無いモデルとなってしまった。

なお，以上の実験に使ったRコードはエントリー最後に貼ってある。

b. アイテムごとに出現確率が異なる場合

では，出現確率が異なる場合はどうだろう？同じように実験してみよう。それぞれのアイテムの出現確率を $p_i$ とする。ただし，

$\Sigma_{i=1}^{m}p_i=1$

とする。n = m の場合は完全コンプモデルで，m 種類全てのコンプに必要な期待回数 $E[X(m)]$ は，

$E[X(m)]=\Sigma_{i=0}^{m-1}(-1)^{m-1-i} \Sigma_{|J|=i}\frac{1}{1-P_j},\qquad\qquad\qquad\left(P_j=\Sigma_{j \in J}p_j\right)$

であった。n 種類の場合は，

$E[X(n)]=\Sigma_{i=0}^{n-1}(-1)^{n-1-i}{m-i-1 \choose m-n} \Sigma_{|J|=i}\frac{1}{1-P_j},\qquad\qquad\qquad\left(P_j=\Sigma_{j \in J}p_j\right)$

と表される。

まず初めに m = 20 に固定し，通常アイテムとレアアイテムが半々ずつ状況を考える。通常とレアアイテムの出現確率の比率を変えた以下の設定における，部分コンプ種類数 n の値ごとのコンプに必要な期待回数のテーブルを示した。

1. レアが 10倍出にくい場合（レア：10個，通常：10個）

（※ 例えば下のテーブルの 6 番目の 7.834 という数字は，6種類のアイテムをコンプするのに必要な期待回数を示している。この場合，期待回数は n の前後で変化は少ない。）

1-5	1.000	2.091	3.293	4.627	6.126
6-10	7.834	9.816	12.168	15.053	18.761
11-15	23.906	31.266	41.474	54.932	72.008
16-20	93.397	120.641	157.217	212.192	322.187

2. レアが 50倍出にくい場合（レア：10個，通常：10個）

（※ 期待回数テーブルは n = 10, 11 のところで2倍の変化がある。）

1-5	1.000	2.106	3.345	4.750	6.375
6-10	8.298	10.653	13.690	17.961	25.215
11-15	57.885	109.104	171.658	244.307	329.277
16-20	431.274	558.773	728.773	983.773	1493.773

3. レアが 100倍出にくい場合（レア：10個，通常：10個）

（※ 期待回数テーブルは n = 10, 11 のところで5倍の変化がある。）

1-5	1.000	2.108	3.352	4.769	6.414
6-10	8.374	10.798	13.973	18.575	26.989
11-15	105.131	213.687	339.513	483.760	652.091
16-20	854.091	1106.591	1443.257	1948.257	2958.257

※ 以上の結果より，n = 10 と 11 のところに期待回数のギャップが存在し，かつレアアイテムの確率が低い ( 2. より3. の方が低い) ほどそのギャップが大きいことが伺える。

f:id:doryokujin:20120529191554p:plain

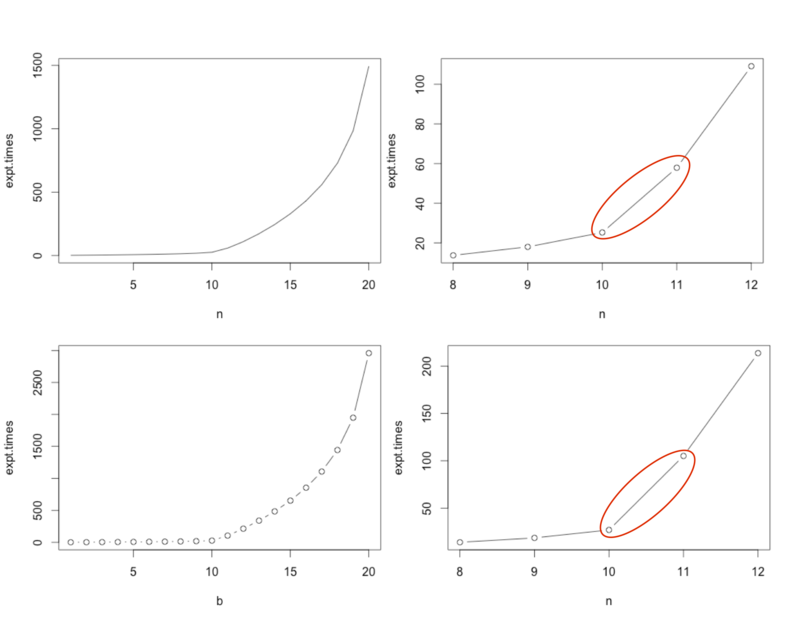
2. （上）と 3. （下）における n の値における推移を図示したものが上の図になる。左は全体 n = 1〜20 で，右は n = 8〜12 での局所的な図である。

今度は通常アイテムが 5 個，レアアイテムが 15個という設定を考えて以下の2つの設定を考えてみる。

4. レアが 50倍出にくい場合（レア：15個，通常：5個）

（※ 期待回数テーブルは n = 5, 6 のところで同じく2倍の変化がある。）

1-5	1.000	2.219	3.779	5.941	9.462
6-10	20.708	37.410	57.170	79.103	103.161
11-15	129.655	159.098	192.223	230.080	274.247
16-20	327.247	393.497	481.830	614.330	879.330

5. レアが 100倍出にくい（レア：15個，通常：5個）

1-5	1.000	2.234	3.843	6.155	10.273
6-10	36.246	71.406	110.771	153.655	200.469
11-15	251.969	309.191	373.566	447.137	532.971
16-20	635.971	764.721	936.387	1193.887	1708.887

（※ 期待回数テーブルは n = 5, 6 のところで同じく 3.6倍の変化がある。）

※ 以上の結果より n = 5 と 6 のところでも，期待回数のギャップが存在することがわかる。また，ギャップ差も n = 10 と 11 の間よりは多少は下がるが大きな変化が無いことがわかる。

f:id:doryokujin:20120529185153p:plain

5. （上）と 6. （下）における n の値における推移を図示したものが上図になる。左は全体 n = 1〜20 で，右は n = 3〜7 での局所的な図である。n が早い段階でも期待回数のギャップは起こる。

考察：期待回数のギャップをうまく利用しよう

上記の現象はよく考えてみると特別な事では無い。n = 10, 11 や n = 5, 6 のところのギャップは通常アイテムを全部集めて終わり，いざレアアイテムを（1つでも）集めようというところなのだ。

今回の実験結果は，必ずしも全てのアイテムを集めようとしなくても，レアアイテムの出現確率を十分小さくしておけば，それが1つでも出すためには多くの回数を要することを数値を持って示している。

この結果を受けて提供側が有利となる数学的ゲームデザインは通常アイテム n_a 枚とレアアイテム n_b 枚が存在する設定の下で，

『部分コンプ回数 n は必ず少なくとも1枚のレアアイテムが含まれるようにせよ。i.e. n_a < n に設定せよ。』

ということである。上の例では「 n = 11 または n = 6 をもってコンプとせよ」ということである。この設定では，ユーザーはコンプまで残り1枚のところまでは非常にスムーズに集まるのに，最後の1枚だけがなかなか集まらないという状況になるだろう。

このゲームデザインにおいては全ての n において期待回数が計算できる。提供側はアイテムの出現確率を調節することによって，部分コンプまでの期待回数を全て計算できることこそが，数学的ゲームデザインの何よりの魅力である。上記の結果も考えてみれば当たり前の事であるが，数値を持って示せるのは非常に強力である。

次回は，2. の『同種類のアイテムを一定数集める』ことによってコンプリートとされるモデルと考える。この問題と同型の数学モデルは「Birthday Paradox」を一般化したものである。この問題に対しては，同種類のアイテムが

2 枚集まる（ダブる）
3 枚集まる（ダブる）

状況が何回目で起こりやすくなるのか，初めて2枚ダブる期待回数は，などと言った問題を考える。確率の話では例えば365種類のアイテムがあれば，23 回ガチャを回したユーザーの 1/2 はアイテムが2枚ダブっており，89回ガチャを回したユーザーの 1/2 はアイテムが3枚ダブっているといったことが示せる。また，4枚以上集まる状況は定式化ができても数値計算が難しくなってしまうことを紹介する。

※ a. で用いた R のコードはこちら。

※ b. で用いた R のコードはこちら。